官方咨询热线：
400-8007-226
资讯中心
03.31
近年来，高精度数值仿真与结构分析技术在复杂机械系统和柔性结构领域得到了广泛应用。然而，传统的刚柔耦合计算方法存在以下核心难题：
柔性体大变形、塑性应变等问题难以用显式方法有效处理。
显式求解方法数值不稳定，需使用极小时间步长，导致计算效率低下。
约束求解复杂度高
传统罚因子法易导致计算发散。
万向锁（Gimbal Lock）现象
传统欧拉角、卡尔丹角方法限制了旋转自由度的表达能力。
为了解决上述问题，迈曦研发团队通过研究发现，在刚柔耦合问题中，连接单元的建模精度和求解方法直接影响整体系统的仿真效果，尤其是在涉及旋转自由度的机械组件（如铰链、关节机构等）时，合理的连接单元对于系统运动特性、力学响应和数值稳定性至关重要。在众多连接单元中，HINGE连接器因其能够模拟旋转自由度约束，在刚柔耦合分析中扮演着至关重要的角色。然而，现有的HINGE连接单元多基于显式求解方法，容易受到时间步长、数值耗散等因素的影响，导致计算不稳定甚至无法收敛，因此提出了一种基于隐式柔性结构求解器的HINGE连接器计算方法，该方法结合四元数表示、牛顿-拉弗森迭代与拉格朗日乘子法，有效提升了HINGE连接单元在多刚体、多柔体系统中的计算稳定性与效率，为高精度结构仿真提供了更可靠的解决方案。下面通过一些具体案例展示这一算法的创新点和优势：
基础理论的正确性及高效性验证
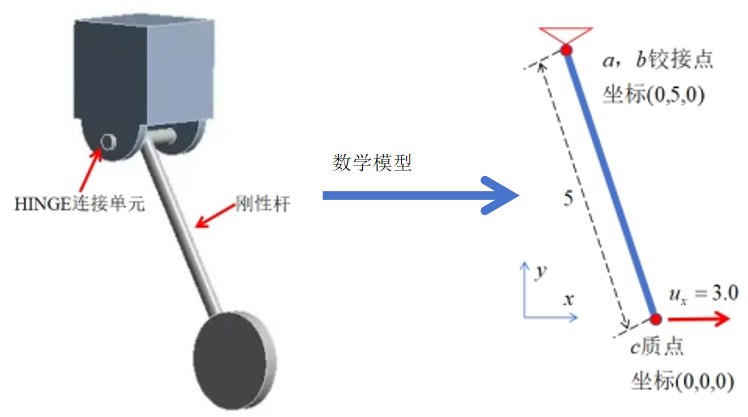
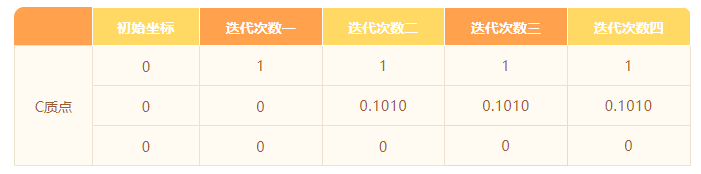
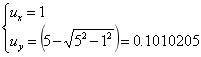
为验证基础理论的正确性及计算方法的高效性，我们采用了一个刚性单摆算例来验证，其模型如下所示： 图为单摆算例的数学模型 得到以下计算结果： 对此算例，只考虑c点的运动，我们同样可以简单得到其理论解： 对比迭代结果与理论结，我们可以看到，对于一个大转动问题，其仅迭代一步即可收敛，这证明了该算法的正确性和高效性。
为验证该算法的实际应用性，我们采用了多体系统中常见的发动机活塞和铲斗提升运动模型进行验证，其计算结果如下所示：
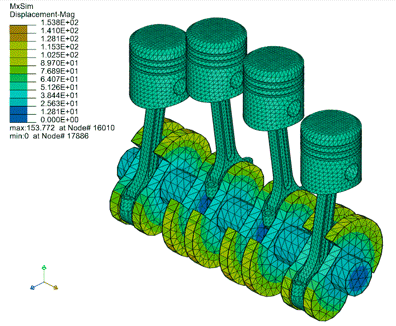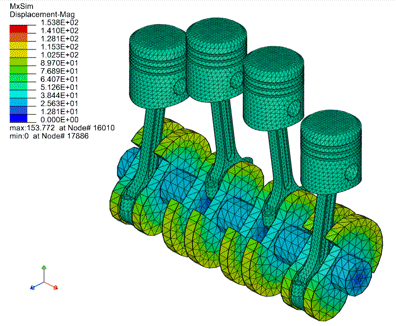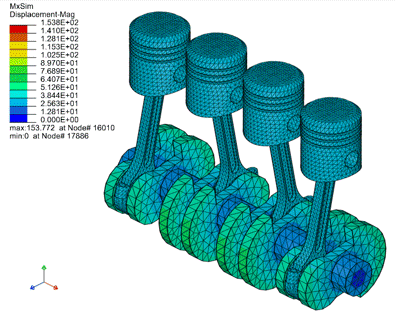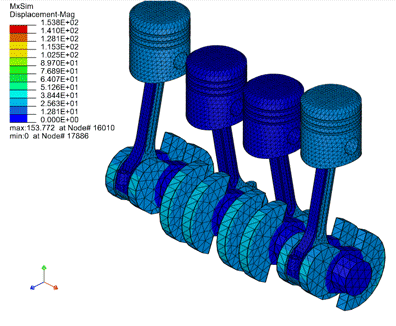
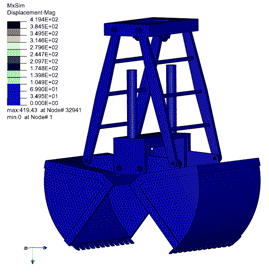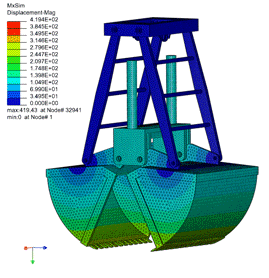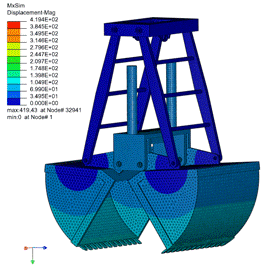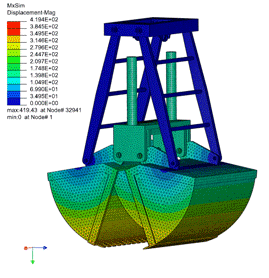
图为发动机活塞运动模型 图为铲斗提升运动模型 这两个工程模型证明了我们算法具有以下优点： 用四元数表示空间旋转，避免万向锁问题 ◆旋转更新可通过四元数乘法实现，计算效率更高； ◆计算过程中减少矩阵存储开销，降低内存消耗。 采用转动伪矢量构建旋转矩阵，提升计算精度 ◆基于欧拉原理，将 HINGE 连接器的空间大转动分解为旋转轴和旋转角度； ◆构建转动伪矢量，将其斜对称展开得到自旋张量； ◆将自旋张量通过指数展开得到旋转矩阵。 旋转矩阵线性化，提高收敛性与计算稳定性 ◆推导旋转矩阵的一阶变分，并进行线性化近似，提升求解稳定性和效率。 采用牛顿-拉弗森法-拉格朗日乘子法，优化约束求解 ◆采用牛顿-拉弗森法处理非线性方程，提高计算收敛速度； ◆结合拉格朗日乘子法处理约束方程，避免罚因子对计算结果的影响； ◆直接提取乘子，计算约束反力与约束力矩，实现高精度力学仿真。 未来，我们还将不断深入技术攻关、优化算法，以适应更复杂的工程需求，推动高精度结构仿真技术的发展。
全国服务电话
技术支持：
合作咨询：
